History of Mathematics Project | Babylonian Mud Wall Tablet

History of
Mathematics

Project

around 2000–1900 BCE

Babylonian Mud Wall Tablet

The mathematics of mud walls

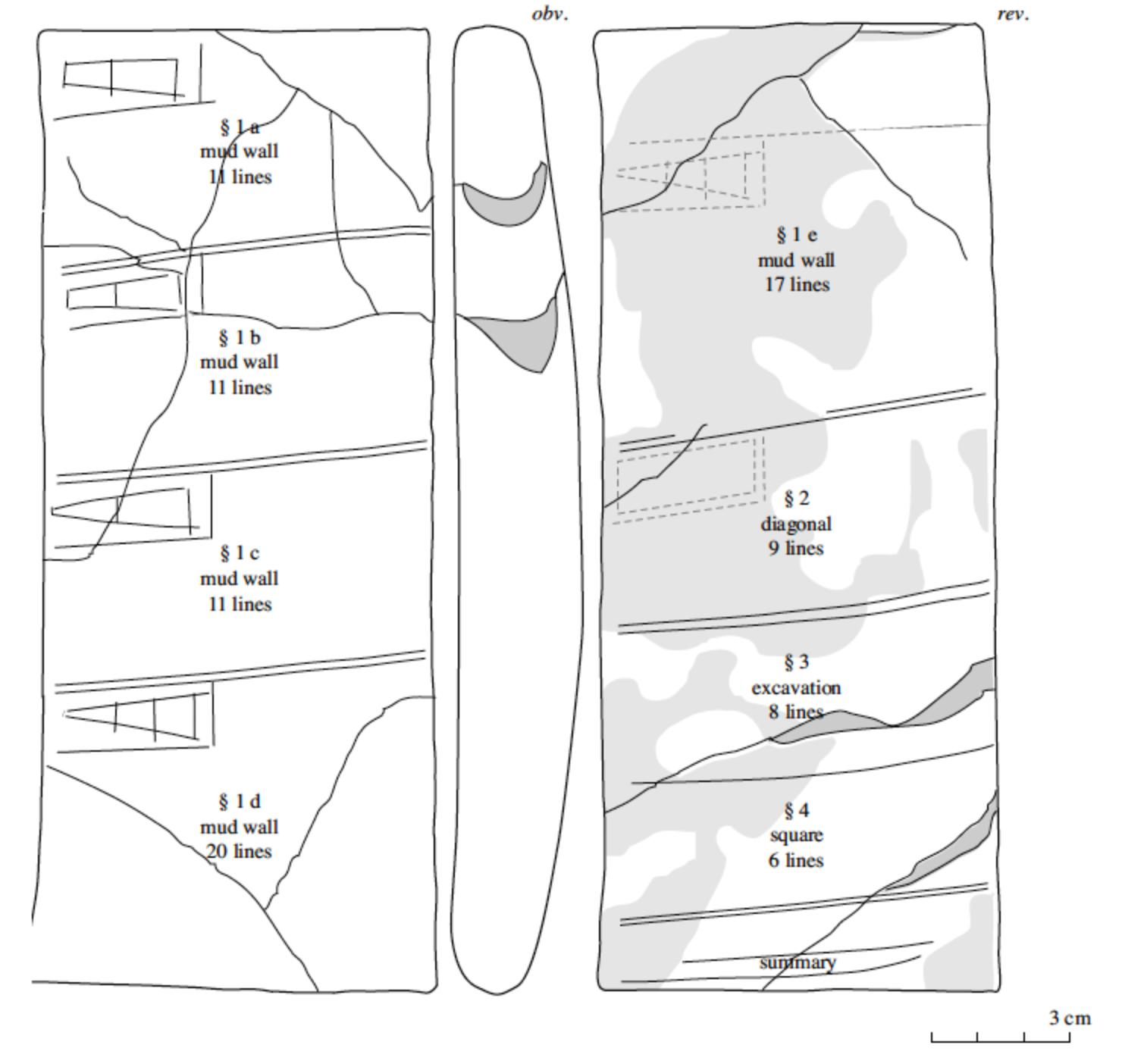
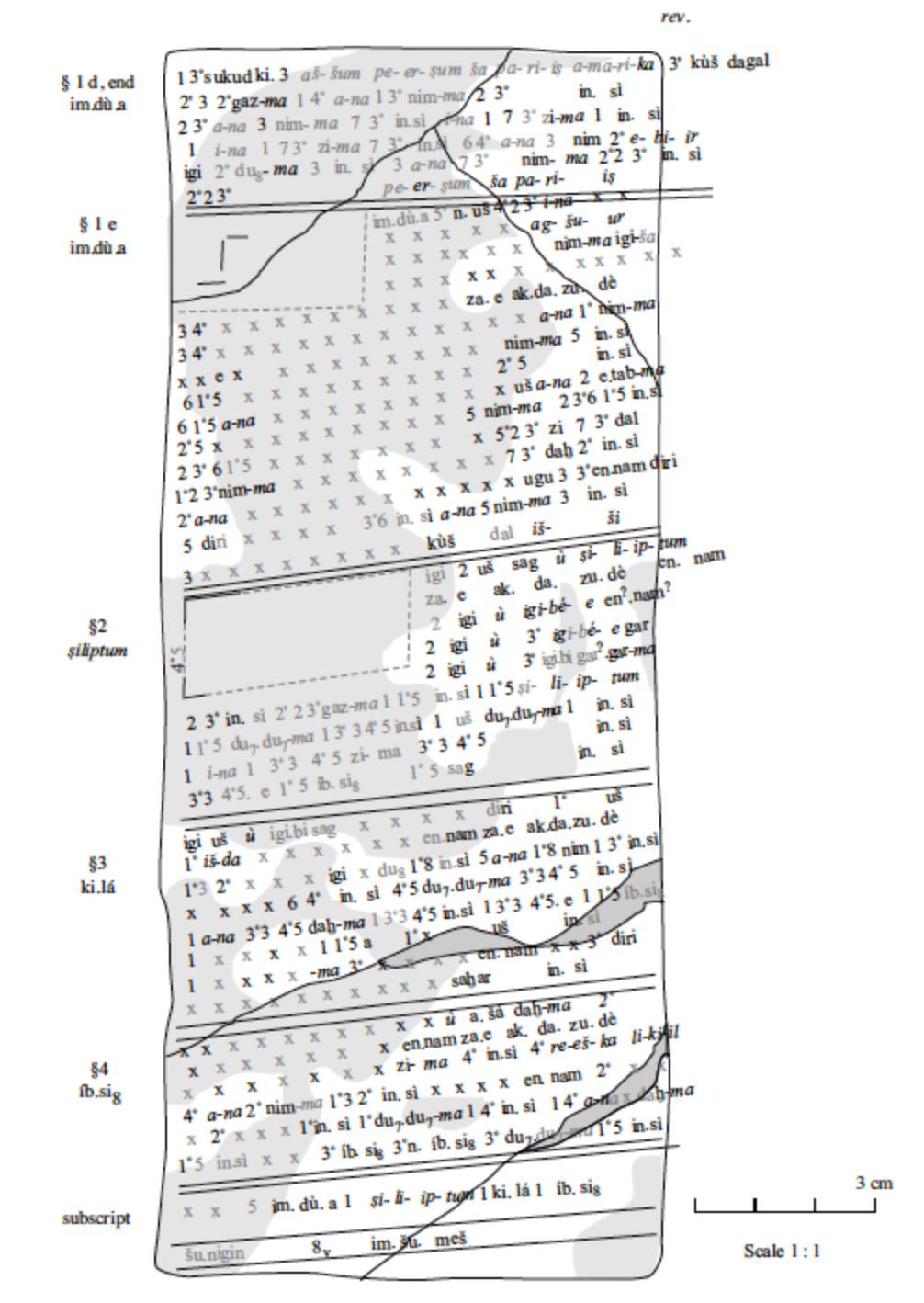
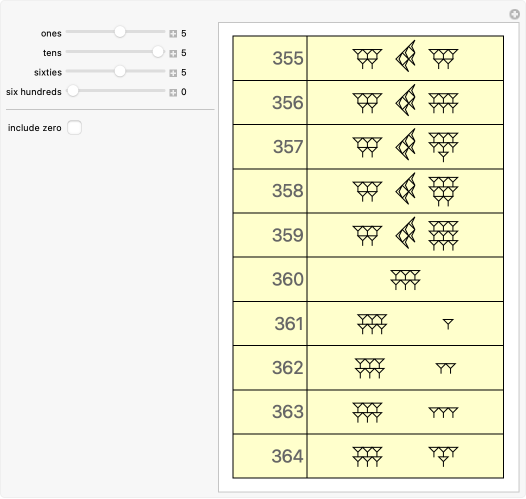
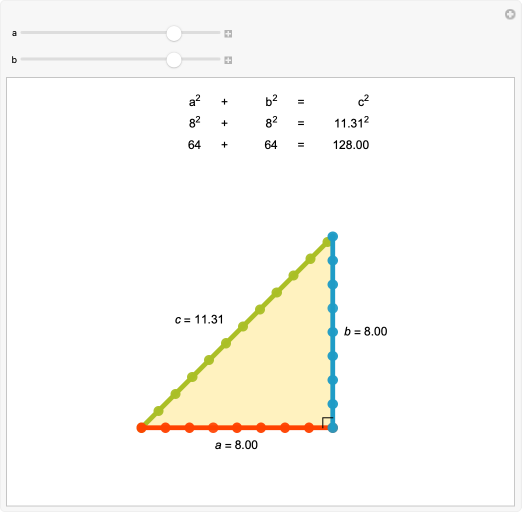
Tablet MS 3052 dates from ancient Sumerian civilization around 2000–1900 BCE and probably originates from the city of Larsa. It contains eight mathematical exercises, including several drawings of subdivided trapezoids and triangles. Most problems are framed in terms of mud walls partitioned into two or more separate layers. Examples of problems include repairing a breach in a wall with mud from the top of the wall, measuring the thickness of a wall by drilling a hole through it and computing the dimensions of a rectangle comprised of two triangles, each corresponding to the (3, 4, 5) Pythagorean triple.

Problems about trapezoids or triangles divided into two or more smaller parts by transversals parallel to the base were popular in Old Babylonian mathematics. Such problems led to systems of linear or quadratic equations. One type of problem for divided trapezoids led to the equation a² + b² = 2 c². Amazingly, old Babylonian mathematicians could find solutions in integers to both this equation and the similar equation a² + b² = c² (as seen in section 2 of this tablet) at least 1,200 years before Pythagoras.

Artifact dimensions

21.0 cm × 8.2 cm × 2.9 cm

Original artifact location

Larsa (historical name), Iraq (current name)

Current artifact location

Oslo, Norway

Catalog number

MS 3052

Timeline

Interactive Content

Computational Explanation

Tablet MS 3052 contains eight mathematical problems—four on each side—with drawings of subdivided trapezoids and triangles made as problems applied to mud walls partitioned into two or more separate layers:

Problem § 2 on the reverse of the tablet:

… concerns a rectangle and its diagonal. Unfortunately, the text of that problem is poorly preserved:

Luckily, the problem's similarity to the text of a different tablet (MS 3971 § 3a–e) allows reconstruction of the text:

The extant portion of the badly preserved drawing seems to depict a (slightly tilted) rectangle with no diagonals drawn. Happily, the question portion of the problem is well preserved and asks the reader to find the dimensions of the length b, front a and diagonal c of the rectangle:

Out[]=

… when a number called the igi is equal to 2. Written in the sexagesimal (base-60) number system of the Babylonians, the value of the igi is written as:

In[]:=

[◼]	AncientNumberRepresentation

[2,"Babylonian"]

Out[]=

The solution procedure described on the tablet constructs the diagonal length c as (igi + igi.bin)/2, where igi.bin is the reciprocal of the igi. Given that igi  2, igi.bin has value 1/2  0; 30 in sexagesimal:

In[]:=

RealDigits

,60

Out[]=

{{30},0}

Therefore, c is given by:

In[]:=

2

Out[]=

Written in sexagesimal, this equals 1; 15:

In[]:=

RealDigits

,60

Out[]=

{{1,15},1}

… and is written in cuneiform as:

In[]:=

[◼]	AncientNumberRepresentation



,"Babylonian"

Out[]=

Solving the Pythagorean theorem



for a and plugging in a length

b1

(as stated on the tablet) and

c5/4

(as just computed) then gives:

In[]:=

Out[]=

… or, in cuneiform:

In[]:=

RealDigits

,60

Out[]=

{{45},0}

Because the greatest common divisor

GCD(a,b,c)

is 1/4:

In[]:=

GCD

,1,



Out[]=

… dividing by 1/4 (or, equivalently, multiplying by 4) identifies the triple (a, b, c) as a multiple of the basic Pythagorean triple (3, 4, 5):

In[]:=

4

,1,



Out[]=

{3,4,5}

An alternate interpretation of the length 1 as meaning 1; 0 (60) (which is possible, given that Babylonian number system lacks an analog of a decimal point or a positional 0, thus making number representations ambiguous up to powers of 60) would instead give the Pythagorean triple:

In[]:=

60

,1,



Out[]=

{45,60,75}

… or in sexagesimal:

In[]:=

RealDigits[{45,60,75},60][[All,1]]

Out[]=

{{45},{1,0},{1,15}}

Problem § 1c of the tablet:

… which is one of a number of problems involving a wall with a hole drilled through it, also involves a Pythagorean triple. In this case, the triple involved is (8, 15, 17), whose elements can be directly verified to satisfy the Pythagorean theorem:

In[]:=

8^2+15^217^2

Out[]=

True

Other Resources

Wolfram Demonstration
Babylonian Numerals

Wolfram Demonstration
Pythagorean Theorem

Additional Reading

Friberg, J. "MS 3052. A Single-Column Mathematical Recombination Text." § 10.2 in A Remarkable Collection of Babylonian Mathematical Texts: Manuscripts in the Schøyen Collection: Cuneiform Texts I. New York: Springer, pp. 254–274 and 493, 2007.