2500 BCE–1612 CE
Funding for this project generously provided by Overdeck Family Foundation
Games of chance have always fascinated humanity. Rolling dice has been performed in the most diverse parts of the world, and in all eras: in prehistoric America, in ancient China, India, Africa, Europe… everywhere. The evolution and spread of ancient games of chance across cultures and time provide a unique perspective on the origins of the mathematical theory of probability.
Some materials and objects used in antiquity as casting devices include seashells, knucklebones of sheep, seeds, pebbles, clay, metals, glass, ivory, nutshells, sticks, bamboo strips, spinning tops (teetotum) and, of course, regular polyhedra. Remember that a polyhedron is a three-dimensional solid that consists of a collection of polygons joined at their edges. Polyhedra form in the natural world in some crystals and have been of interest to many civilizations in art, architecture and games of chance.
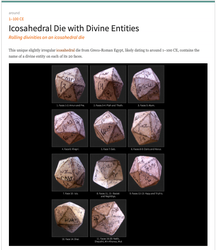
A number of icosahedral dice made in various materials have survived from the Hellenistic and Roman periods, usually from ancient Egypt when known. The ones depicted above are only a few from the Metropolitan Museum of Art in New York. They may have been used in conjunction with an oracle inscribed on a pillar set up in a public place. The polyhedron was thrown in order to choose a letter at random. One consulted the inscription to find the matching letter and read the oracle's response. There would be 20 oracular messages, each beginning with a letter of the alphabet that corresponded to one side of the die.

4. Face 6: Khepri. 5. Face 7: Geb. 6. Faces 8–9: Osiris and Horus.
This unique, slightly irregular icosahedral die from Greco-Roman Egypt, likely dating to around 1–100 CE, contains the name of a divine entity on each of its 20 faces. The die was likely thrown to determine the best Egyptian deity from whom to seek assistance. Adopting this interpretation, press the following button to roll a randomly selected deity and give an indication of the deity's main domains of influence:
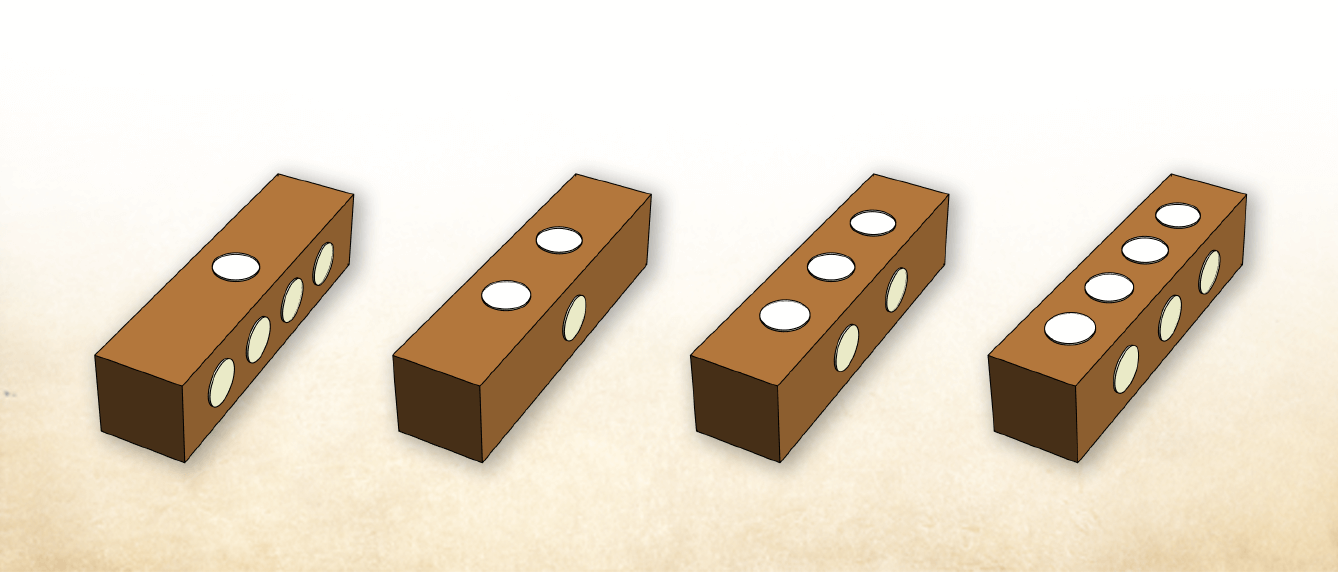
In the 1970s, an Italian expedition to the Burnt City (Shahr-e Sukhteh) explored the graveyard of this ancient city located in the southeastern part of Iran, midway between the Middle East and India. Among many other interesting artifacts, they found a set of 4 elongated dice and 27 tokens lying inside a basket placed near the pelvis of a human buried in a pseudo-catacomb (grave 7311; see schematic below). Dating of the dice shows they were crafted about 4500 years ago.

While the Burnt City dice have six sides, they were numbered along only the four rectangular faces:
These dice and tokens were used along with a gaming board measuring 33.2 cm long and 12.0 cm wide to play the Game of Twenty Squares, a two-player strategy race board game that was very popular in ancient Mesopotamia. The following figure (adapted from Piperno and Salvatori, 1983) schematically illustrates the board and the location in grave 731 where it was found:
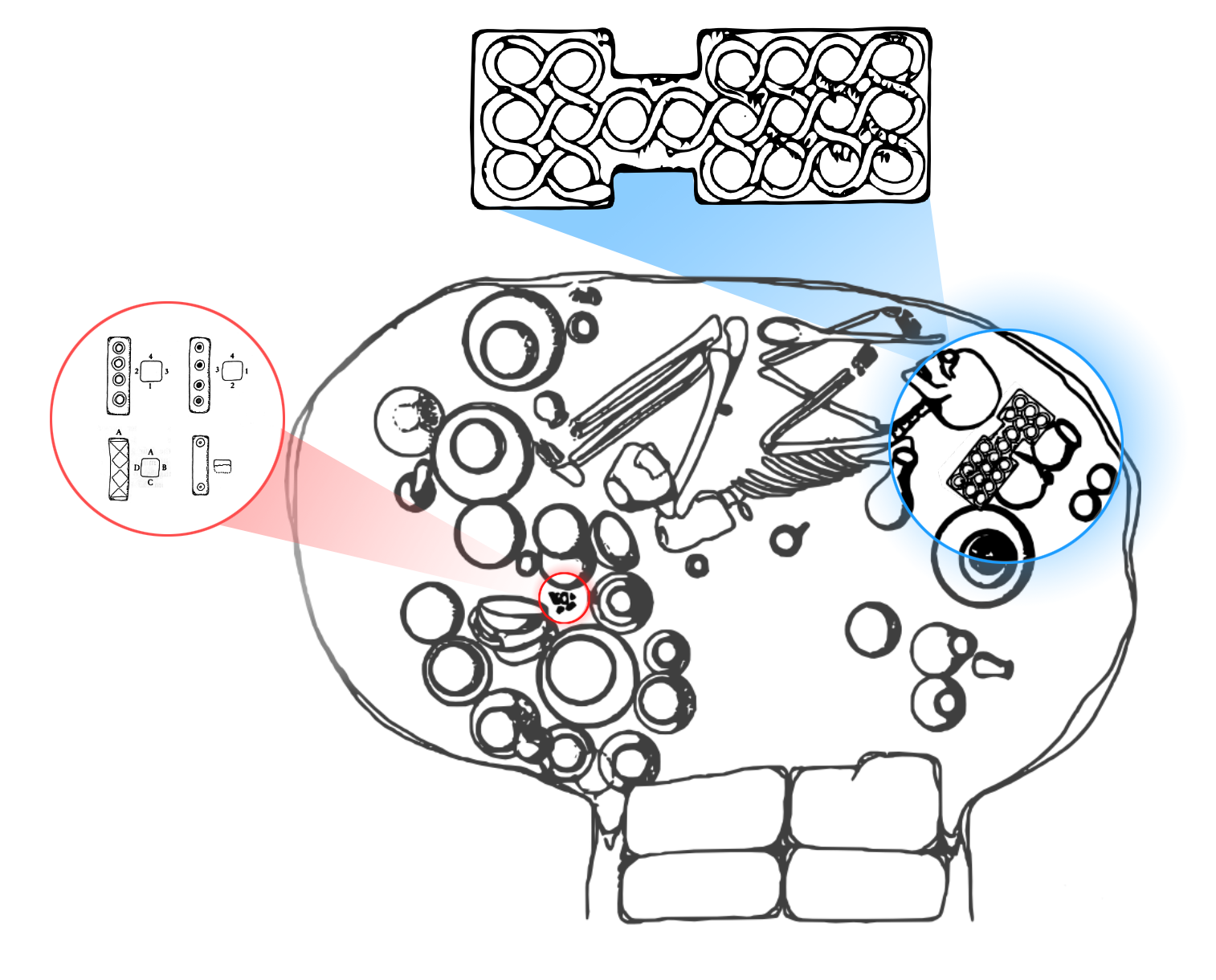
The game board was adorned with a knotted snake carved in relief and is identical in layout to a board found in the Royal Cemetery at Ur (British Museum item #120840), which has been dated to 2600 BCE. While the Ur board is identical in form to the Burnt City board, it is much more regally adorned, including many beautiful and intricate geometric patterns:

Interestingly, while the Burnt City dice are shaped like elongated boxes, the Ur dice are in the form of a tetrahedron, the four-sided Platonic solid:

The historical relationship and evolution between different shapes of four-sided dice is not known. However, practical experimentation suggests that attempting to pick up a tetrahedral die by its apex can be challenging, meaning the elongated dice are easier to grasp. If the tetrahedral dice had numbers written on each face, as the elongated four-sided dice do, they would have the disadvantage that the number rolled would lie facedown and hence be hidden underneath the die. However, precisely to avoid this problem, two of the four corners of each Ur die are marked with a white blob, meaning when four of them are thrown, a total of 0 to 4 blobs are obtained.

While the Game of Twenty Squares is the world's oldest known board game, it can still be played today, since its rules have been deciphered by Dr. Irving Finkel, assistant keeper of ancient Mesopotamian script, languages and cultures in the Middle East department at the British Museum.

Modern dice are shaped like a cube and therefore roll a number between 1 and 6 inclusive. The earliest known dice from Burnt City, however, had an elongated shape and rolled a number from 1 to 4. Explore the faces of a four-valued die from the Burnt City and incrementally morph it from its long, skinny box shape to a modern six-sided cubical die:
This type of elongated die is still being used in India to play two evolved versions of the Game of Twenty Squares: chaupar and pachisi. Interestingly, pachisi was modified to use a cubic die with a dice cup and patented as "Ludo" in England in 1896. Ludo and its variations are popular in many countries and under various names.

An important aspect of being human is playing games, and the prehistoric tribes of North America are no exception. There are many prehistoric games of North America documented, some of which are racing games too. Stave-dice were the most popular type of die used on the continent:
In Historia del nuevo mundo, originally written in 1653, Father Bernabé Cobo documents that the natives of South America invented some ingenious games of dice. One of the games discussed by Cobo is pichqa, which means "five" in Quechua. It was played with a six-sided die with marks referring to one, two, three, four and five points respectively, leaving one side unmarked.

This cubical die invented in South America originated following a completely different path of reasoning than the six-sided dice found in Europe and Asia. Cubical dice that roll a number between 1 and 6 probably evolved from the astragali, knucklebones of sheep and goats that were used in many games of chance, including the Game of Twenty Squares.

The side visible in this photograph has a Twenty Squares gaming board. The other side has 30 squares for the Egyptian game known as senet. These were both games in which two players raced each other for position, using knucklebones or throw sticks as dice to determine each play.
The term knucklebone designates the astragalus, a small bone found within the tarsal joint of hooved animals like sheep and goats. It was used as a randomizing device because it has four long sides on which it can land when cast, with the numerical value assigned to the side facing up. Imitations of astragalus bones were also made from wood, clay, ivory, stone and metal.
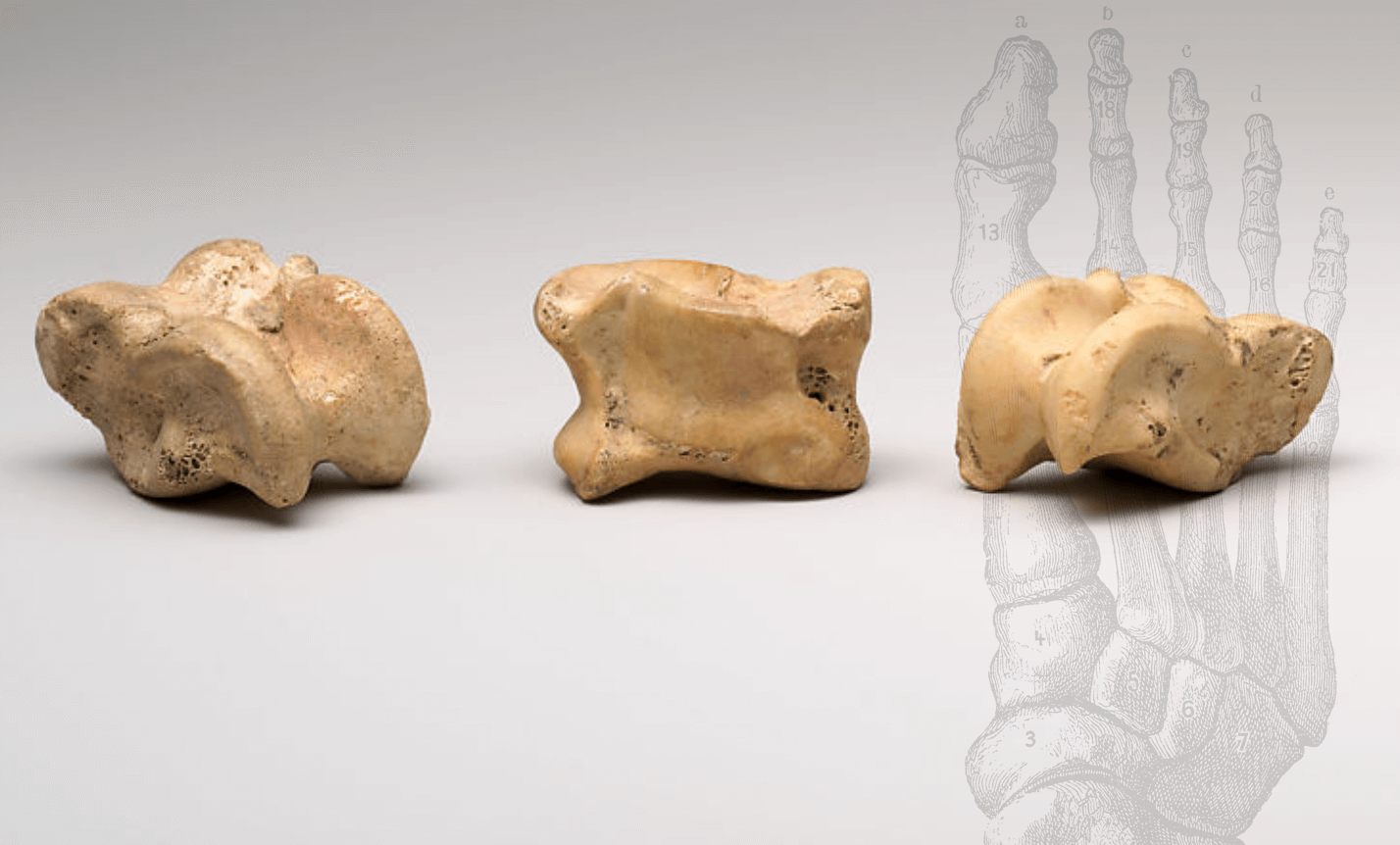
Geography: From Egypt, Upper Egypt, Thebes, Asasif, Courtyard CC 41, Pit 1, Chamber B, MMA excavations, 1915–16.
In Egypt, these are better attested from the 17th Dynasty on, which is likely related to the introduction of the Game of Twenty Squares. Egyptians adopted astragali to play senet, and these are the only casting devices represented in New Kingdom playing scenes.

Cubic dice have been in use in the Near East since the third millennium BCE, with different systems used at different times for distributing the points or pips. The numbering of the opposite sides (1–6, 2–5, 3–4), each adding up to 7, comes into more general use only later, as reflected by the dice above. During the Greco-Roman period, cubic dice became more common and gradually replaced throwing sticks and knucklebones for use with board games.

Dice were the most popular game among Roman soldiers. "The die is cast" is the famous phrase attributed to Julius Caesar to signify how it is not always possible to change the fate of a battle. Games of dice were also a favorite pastime at banquets and other social occasions. Small round boxes were used as throwing cups to prevent unfair manipulation of the dice.

"And it must be said that there must be three cubic bodies with six identical sides, each of which is the same size as the other and whose square surfaces should also be the same. If it were otherwise, the die would not fall as well on one side as it would on the other, and that would be more of a fraud than a coincidence. And that is why it is one of the methods of cheating, as we will report later, that people use fraudulently to make false dice. And on each of these six square sides there must be pips arranged as follows: 6, 5, 4, 3, 2 and 1, so that each die has a total of 21 pips and thus all three dice have 63 pips. And the pips should be arranged in this way: opposite the 6 the 1, opposite the 5 the 2, and opposite the 4 the 3." (Excerpt from the Libro de axedrez, dados e tablas, Fol. 65v, Escorial Monastery Library, Madrid.)

Alfonso X (1221–1284), the king of Castile, commissioned the Book of Games, the first encyclopedia of games in European literature. Under Moorish influence, the Iberian peninsula was a somewhat enlightened region of Europe compared with other parts of the continent. Alfonso personally supervised a group of Jewish, Moorish and Christian writers whose task was to produce a series of books on all of the most important topics of his time: history, law, religion, astronomy and games!

The book is one of the most important documents for researching the history of board games. It consists of 97 folios illuminated with a total of 150 miniatures. The text is a treatise that addresses the playing of three game types: games of skill, or chess-like; games of chance, or dice; and backgammon-like, which combine elements of both skill and chance. These games are discussed in the final section of the book at an astronomical and astrological level.

The second part of the book was dedicated entirely to games of chance. Gambling has been always a high-risk activity and the games of dice covered in the book were forbidden several times in history. Against all odds, these games survived from generation to generation for hundreds of years. Experience the thrill of playing azar, triga, riffa, marlota, High Rolls and As Many on One as on Two!
The three wheels of fortune depicted below are from Triompho di Fortuna by Sigismundo Fanti. Published in January 1526, the book was the first illustrated fortune-telling book to appear after the popular Libro delle sorti (The Book of Fates) of Lorenzo Spirito, which in turn was first published in 1482 and had gone through several editions. Fanti's book functions as a game in which the seeker follows cues that lead from figures of fortune to houses and then to wheels, spheres and astrologers. The path is determined by either a throw of two dice or the time of day at which the book is consulted.
Another book on fortune-telling dice games was The Dodecahedron of Fortune, attributed to the French medieval poet Jean de Meun and dated to roughly the first quarter of the 14th century. The work regained popularity as a printed text as demonstrated in this 1615 edition:

Since dice were used in gambling, in religious ceremonies and for divination, it is believed that those who used the dice had a good intuitive idea of the likely frequency of various number combinations.

The theory of probability was born when the nobles, in the 17th century, commissioned the scientists of the time to solve the various questions that arise in games of chance, in particular the game of dice. Galileo Galilei's paper "About the Discoveries of Dice" dates from 1596, in which he investigates how by throwing three dice, some scores are more advantageous than others:
Galileo stated that with three dice, there can only be one way of obtaining a 3 (1, 1, 1) and an 18 (6, 6, 6). However, there are three combinations for obtaining a 6—(4, 2, 1), (3, 2, 1) and (2, 2, 2)—which can occur in different orders, making 10 possibilities. There are four combinations for a 7—(5, 1, 1), (4, 2, 1), (3, 3, 1) and (3, 2, 2)—which lead to 15 possibilities. However, although 9 and 12 could be made up in the same number of ways as 10 and 11, from their experience, gamblers claimed that the occurrence of 10 and 11 were more likely! Galileo showed that the total number of possible throws with three dice are 216, and he gave a table of the number of possible throws for a total of 10, 9, 8, 7, 6, 5, 4 and 3, showing that the throws for 11 to 18 were symmetrical with these. In this way, he showed that there were 27 possible throws to obtain a 10, and 25 for a 9.
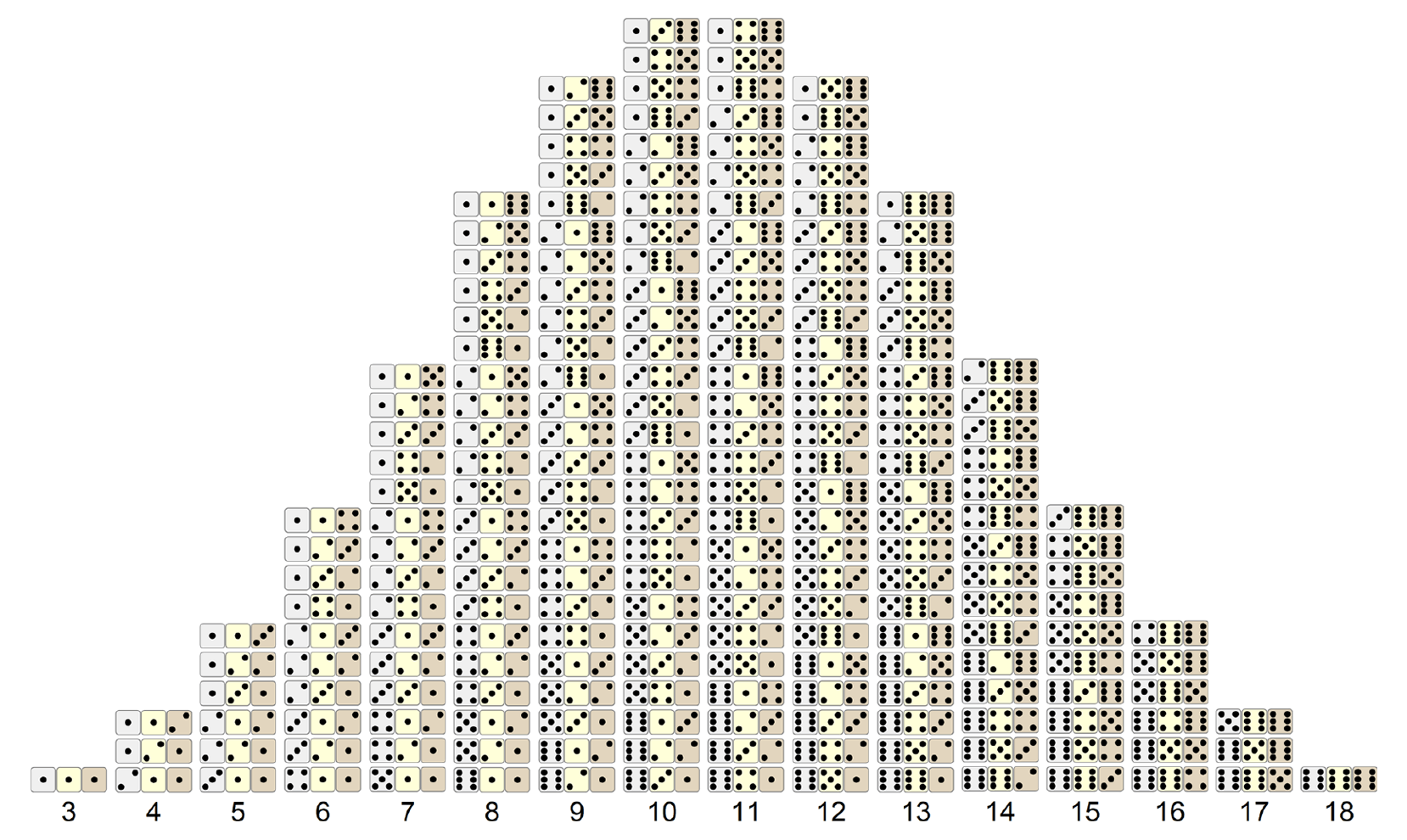
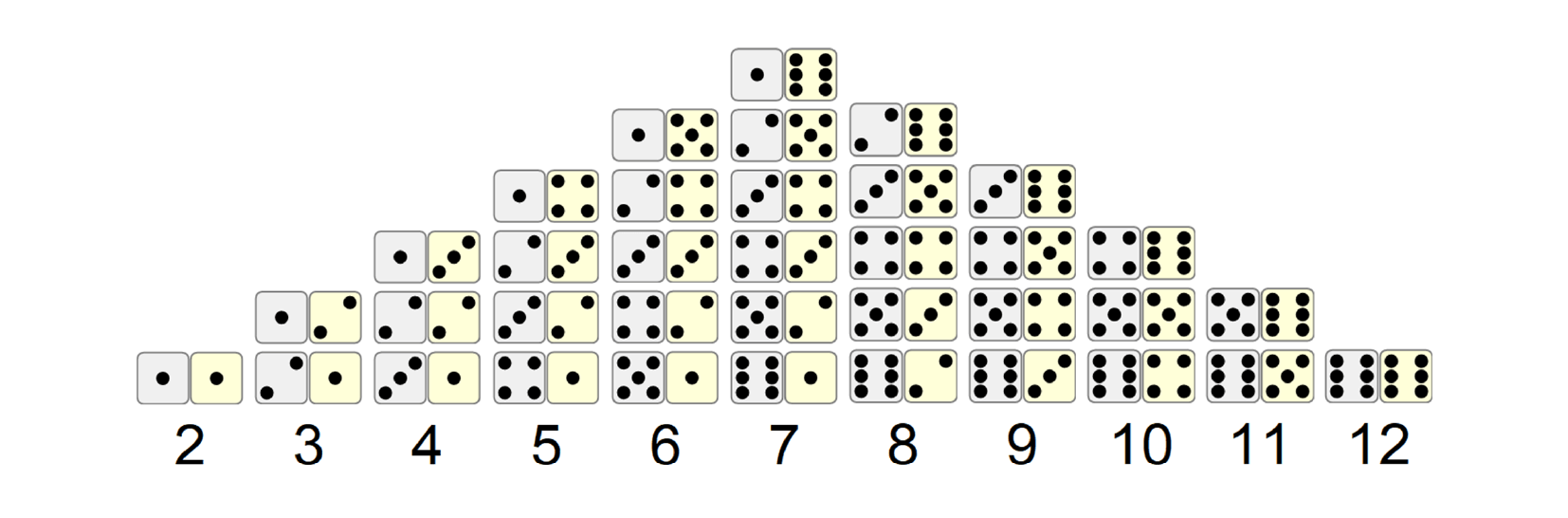
Galileo's solution was already known a century earlier to the mathematician Girolamo Cardano of Pavia (1506–1576). The modern mathematical theory of probability was born in the attempts to analyze games of chance by Cardano in the 16th century, and later by Galileo, Pierre de Fermat and Blaise Pascal in the 17th century. Christiaan Huygens published a book on the subject in 1657, and in the 19th century, Pierre Laplace completed what is today considered the classic interpretation.
Find Out More About
Visit the online History of Mathematics exhibit to learn more!
Further Reading
- British Museum. "Top 10 Historical Board Games." The British Museum Blog, February, 26, 2021. [link]
- Crist, W.; Dunn-Vaturi, A. E.; and de Voogt, A. Ancient Egyptians at Play: Board Games across Borders. Bloomsbury Publishing, 2016.
- Culin, S. "American Indian Games." Journal of American Folklore, Vol. 11, No. 43, pp. 245–252, 1898.
- Culin, S. Chinese Games with Dice. Franklin Printing Company, 1889.
- Culin, S. Games of the North American Indians. Courier Corporation, 1975.
- Culin, S. "Hawaiian Games." American Anthropologist, Vol. 1, No. 2, pp. 201–247, 1899.
- Culin, S. Korean Games with Notes on the Corresponding Games of China and Japan. University of Pennsylvania, 1895.
- David, F. N. Games, Gods, and Gambling: A History of Probability and Statistical Ideas. Courier Corporation, 1998.
- Galilei, G. Sopra le scoperte de i dadi. Museo Galileo. Museo Galielo. [link]
- Gentile, L. and Margarita, E. "La pichca: oráculo y juego de fortuna (su persistencia en el espacio y tiempo andinos)." Bulletin de l'Institut français d'études andines, Vol. 27, No. 1, pp. 75–131, 1998. [link]
- Gorroochurn, P. Classic Problems of Probability. Wiley, 2012.
- Gorroochurn, P. "Some Laws and Problems of Classical Probability and How Cardano Anticipated Them." Chance, Vol. 24, No. 4, pp. 13–20, 2012. [link]
- Kendall, M. G. "Studies in the History of Probability and Statistics: II. The Beginnings of a Probability Calculus." Biometrika, Vol. 43, No. 1/2, pp. 1–14, 1956.
- Pereira dos Santos, C.; Neto, J. P.; and Nuno Silva, J. "Babilónia–Ur, 10 Livros, 10 Regiões, 10 Jogos para aprender e divertir-se." Edimpresa, Norprint, June 2008. [link]
- Piperno, M. and Salvatori, S. "Recent Results and New Perspectives from the Research at the Graveyard of Shahr-i Sokhta, Sistan, Iran." Annali Istituto Universitario Orientale, Vol. 43, pp. 174–191, 1983.
- Schädler, U. and Calvo R. (Eds.). Das Buch der Spiele. Münster, Germany: LIT Verlag, 2009.
- Valdez, L. M., and Bettcher, K. J. "Pichqa and Pisqoyñu: Inca Gaming Paraphernalia from Tambo Viejo, Peru." Ñawpa Pacha, Vol. 40, No. 1, pp. 119–132, 2020.
- Vallverdú J. "Probability, History of." In International Encyclopedia of Statistical Science (Ed. M. Lovric). Berlin, Heidelberg: Springer, pp. 1126–1128, 2011.
- Voorhies B. Prehistoric Games of North American Indians: Subarctic to Mesoamerica. University of Utah Press, 2017.
- Waldorf S. "We Tried Medieval Divination—And It Worked." Getty's Art Stories, 2016. [link]
- Wolynes E. "Rolling the Dice: Guided by the Stars, Math, and God (In That Order)." University of Notre Dame. [link]
- Zischkin T. "Alfonso X's Libro de los Juegos." Thinking 3D. University of St Andrews, 2018. [link]
Additional Links
- Ludii Portal: Home of the Ludii General Game System
- MathWorld—A Wolfram Web Resource: Binomial Distribution
- MathWorld—A Wolfram Web Resource: Central Limit Theorem
- MathWorld—A Wolfram Web Resource: Dice
- RenGeekCentral: Alphonso X: Book of Games: A Game Researcher's Resource
- Rogers, L.: From A Random World to a Rational Universe
- Wikipedia: Chaupar
- Wikipedia: Dice: History of dice
- Wikipedia: History of games
- Wikipedia: Ludo (board game)
- Wikipedia: Knucklebones
- Wikipedia: Libro de los juegos
- Wikipedia: Long dice
- Wikipedia: Pachisi
- Wikipedia: Stewart Culin: World of games
- Wolfram Demonstrations Project: Rolling Multiple Dice"