If you were a worker thousands of years ago, how would you get paid?

You wouldn't be paid in coins, because coins were not invented until around 600 BCE.

You wouldn't be paid in paper money, either, since paper money was not developed until around 960 CE, in China.

In ancient Mesopotamia (pronounced mess-oh-poh-TAY-me-uh) during the Early Bronze Age (around 3000–1200 BCE), people received a grain called barley as payment for their work.

Barley is a grain like wheat. You can cook barley and eat it, like you would eat a bowl of oatmeal, or you can grind it into flour and use the flour to make bread.

Four thousand years ago, a worker in Mesopotamia would have been paid one gur of grain every month. That's about 300 liters of grain (or, when converted to US customary units, 79 gallons). So for one day of work, a person could earn about 10 liters of grain (300 liters divided by 30 days in a month). You probably know what a two-liter bottle of soda looks like. Imagine working all day long, then getting a sack filled with five two-liter bottles of grain as your payment.

If you grind one liter of barley grain, you get a little more than six cups of barley flour (flour is fluffier than grain). That's enough flour to make two loaves of bread the size of the sandwich bread we eat today. Since a worker could earn 10 liters of grain in a day, they could potentially make 20 loaves of bread with the grain they earned in one day! Even if you had a big family, you probably wouldn't want to make 20 loaves of bread every single day!

People would use some of their grain to feed their family. Then they would use the rest for trading, or they would save it for later. In ancient Mesopotamia, grain was like money. People could trade grain for foods like beans, lentils, vegetable oil, dates and onions, or they could buy supplies. Since grain lasts a long time, they could save it for food storage. They could also use the grain they saved to trade for things later, just like we save our money today.

The Mesopotamians traded barley to buy everyday things locally. But large quantities of barley are heavy; the weight of one gur of barley is more than five hundred pounds! If people wanted to save up to buy something expensive, it wasn't practical to store or transport thousands of pounds' worth of barley. So they used silver to trade for more valuable things like sheep, houses or land. Sometimes they used a combination of silver and barley to make purchases.

Barley was so important to the ancient Mesopotamians that a barley grain was used as the smallest unit of length, area, volume and weight. One gur of grain could be exchanged for one shekel (pronounced SHEH-kl) of silver. The word shekel means "to weigh out." A shekel of silver weighed as much as 180 barley grains, or about 8.4 grams. That's only a little more than the weight of one quarter plus one penny:

A shekel was a lump of silver that just weighed 180 grains—that doesn't mean that you could trade 180 actual grains of barley for a shekel! One hundred eighty grains is just a handful. Remember, you would need to trade one gur (over five hundred pounds!) of barley to get a shekel. It would take three donkeys to carry one gur of grain. A shekel of silver was definitely more portable than one gur of grain.

Sixty shekels weighed one mina, or about 1.1 pounds:

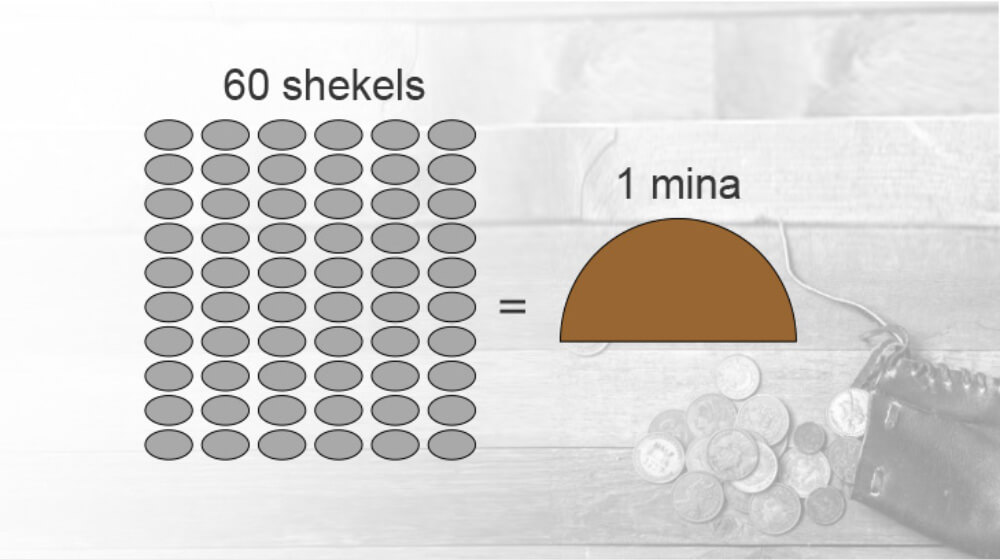
The word mina means "to count." It would take an ordinary worker at least five years to earn that much silver!

Sixty mina weighed one talent:

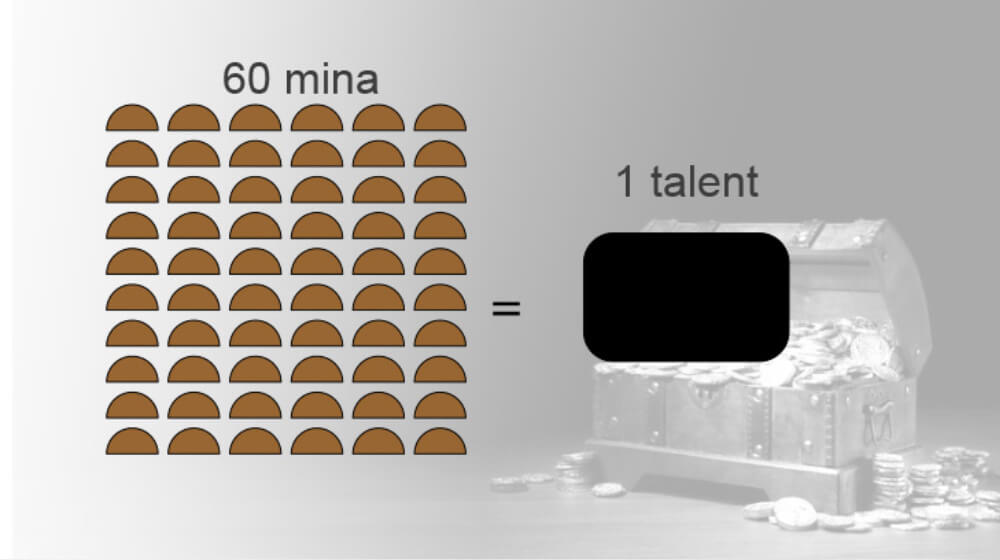
One talent weighed about 67 pounds. A talent was a huge amount of silver. At today's prices, a talent of silver would be worth about $23,000.

Merchants would carry around their own set of weights to help them with trading. Most weights were sort of grain-shaped. Mesopotamian weights were often made of polished hematite:

Mesopotamian weights were often shaped like a sleeping duck, with its neck and head resting on its back:

There are rare examples of Mesopotamian weights in other shapes, but most weights were either grain-shaped or duck-shaped. Here are some unusual examples of Mesopotamian weights: a grasshopper, a shell and a cute frog:

Merchants would use a simple balance scale ️to see how much something weighed. They would put the item to be traded on one side of the scale, and add or subtract weights until the scale balanced:

Other ancient civilizations also used balance scales and weights in the shape of animals:

The Mesopotamians grouped things by the number 60 (60 shekels in 1 mina, 60 mina in 1 talent, etc.). This number system is called base 60, or sexagesimal. The number 60 can be divided by 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60. The divisibility of 60 makes it a perfect base for doing arithmetic. Here are some different ways you can arrange 60 shekels:

Here's one way you can count to 60 on your fingers! Each finger has three bones. Using your right hand, you can count by touching the tip of your thumb to to your 12 finger bones:

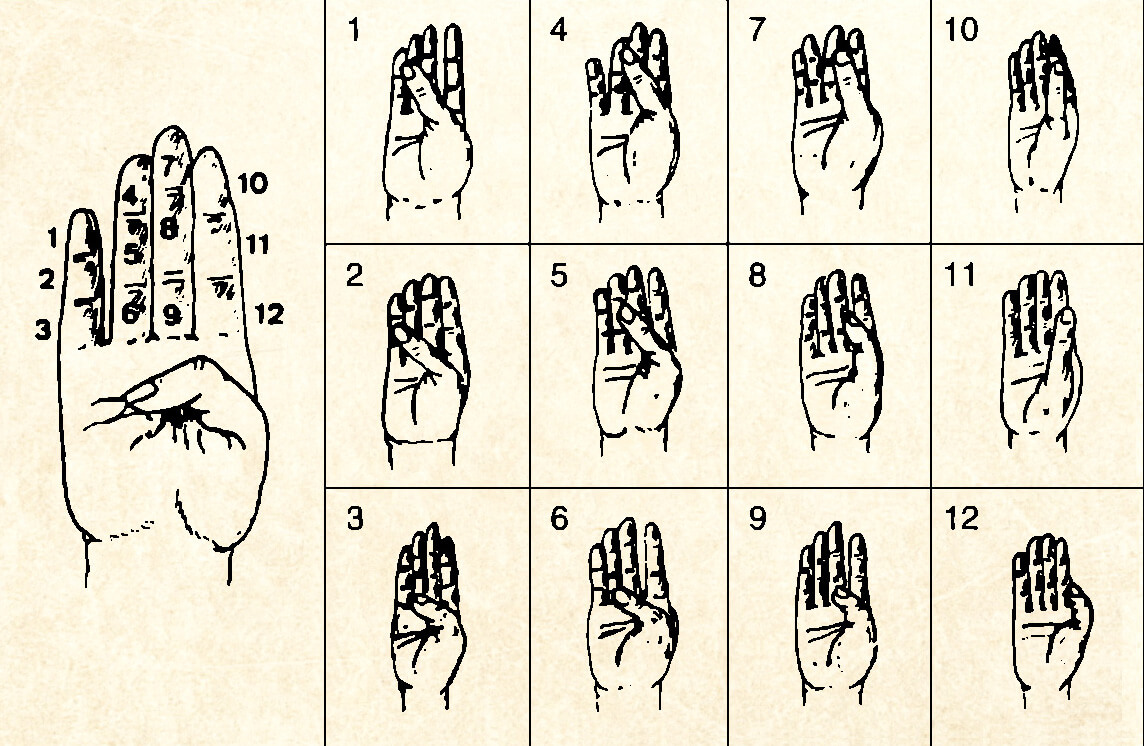
You can use your left hand to keep track of the number of times you've counted to 12. Count to 12 five times, and you get to 60 (12 × 5 = 60). This finger-counting method could explain how the Mesopotamians came to use base 60.

Today, we measure time using base 60 (60 seconds in a minute, 60 minutes in an hour). We also measure angles using base 60 (360 degrees in a circle).

Balance It Yourself!

Mesopotamians would have traded small scraps, lumps or rings of silver when they wanted to buy something valuable. They didn't have standardized coins, so they would have taken various pieces of silver to a merchant to see how much it weighed.

Pretend that you are trading in "grains" of silver. Remember that 180 grains of silver = 1 shekel.

The beam at the top of the scale is like an "equal" sign. As you add more grains of silver on the left side of the scale, the merchant adds duck weights that come in fractions of a shekel so the sides balance:

Most Mesopotamians wouldn't have had much silver. They often had to borrow money to make large purchases, just like people borrow money to buy a house today. However, if they missed a loan payment or couldn't pay their rent, they faced strict consequences.

Here are a couple of little clay tablets describing business deals:

The tablet on the left describes a loan of "one shekel fifty grains of silver, interest 20% from Dumuzi-gamil to Sin-magir, to be repaid after thirty days." So, Sin-magir was borrowing about one month's salary from Dumuzi-gamil. The tablet on the right is a rental agreement. A company of 12 men rented a field for a third of a shekel and four grains of silver. When they didn't pay the rent, they had to pay 10 shekels. They owed two and a half years of rent for missing just one month!

Sometimes, people would cheat by trying to trade a less valuable metal that looked like silver, or they would mix silver with another metal. Merchants could cheat by measuring the value of a person's silver against heavier weights. The Code of Hammurabi, a set of laws from ancient Mesopotamia, details punishments for cheating, theft, fraud and other situations.

When Mesopotamian merchants traded internationally with people like the Egyptians, they had to compare their weights and make conversions to do a fair trade. The Egyptians based their counting system on the number 10 (the decimal system), like we do today, so they used different weights than the Mesopotamians.