History of Mathematics Project | Kepler's Planetary System

History of
Mathematics

Project

1596

Kepler's Planetary System

Nested regular solids model the solar system

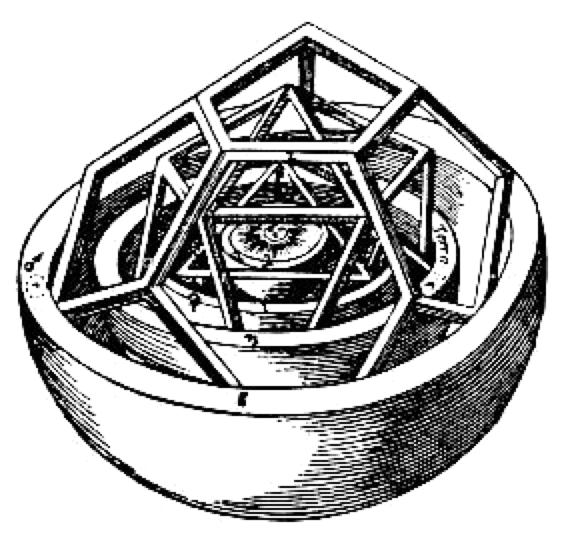
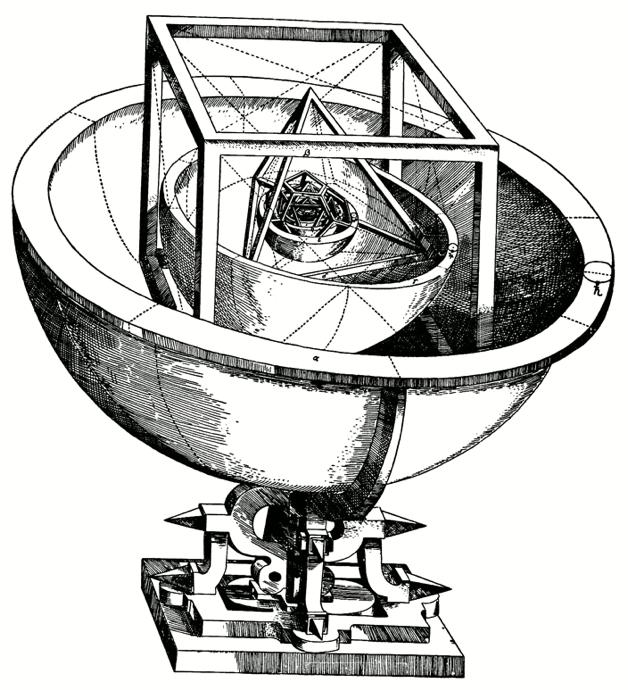
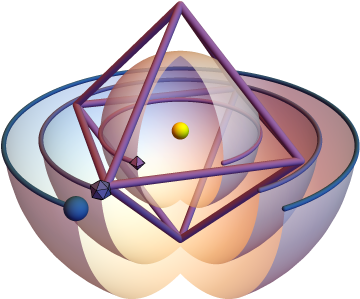
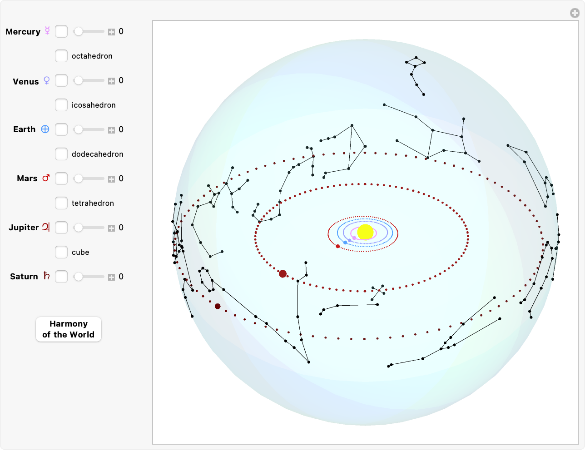
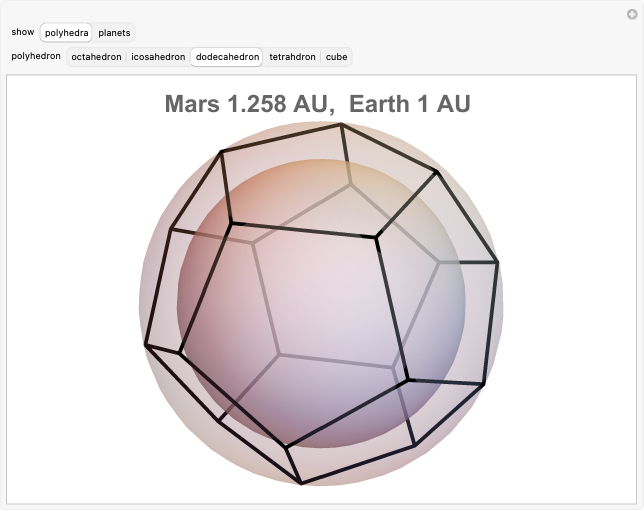
Kepler's 1596 work Mysterium Cosmographicum (The Cosmographic Mystery) envisioned a solar system whose dimensions were based on the nesting of the five regular solids in concentric spheres centered on the Sun. It was therefore a Copernican system representing Kepler's belief that God constructed the universe through geometry.

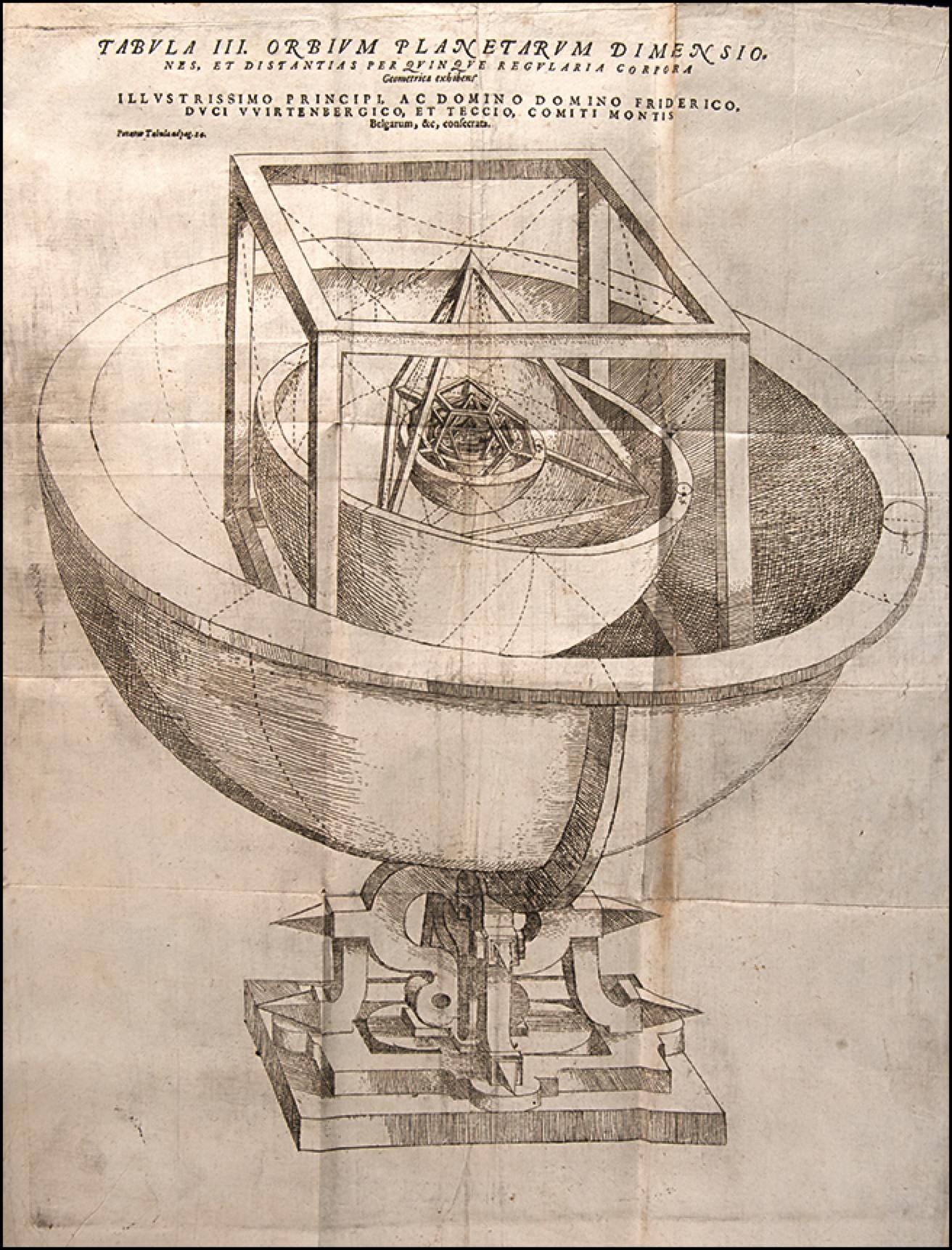
By circumscribing and inscribing the five regular (Platonic) solids on spheres, Kepler obtained a family of nested spheres that was consistent with his geocentric theory of planetary motion. A depiction of this nested polyhedral model appeared in his 1596 work Mysterium Cosmographicum with the title "Tabula III: Orbium planetarum dimensiones, et distantias per quinque regularia corpora geometrica exhibens." While Kepler did not construct a physical model, a number of museums, including the Kepler Museum in Weil der Stadt near Stuttgart, have done so.

Artifact format

Original is a diagram; some museums have constructed physical models

Artifact origin

Graz, Austria

Timeline

Interactive Content

Computational Explanation

Kepler envisioned a solar system in which the orbital distances of the six known planets corresponded to the characteristic radii of a sequence of nested geometric shapes. While Kepler also incorporated astrological and metaphysical considerations into his model, stating, "The mathematical things are the causes of the physical because God from the beginning of time carried within himself in simple and divine abstraction the mathematical objects as prototypes for the materially planned quantities," its underlying foundations were purely geometrical. Kepler’s planetary system seems to be a direct outgrowth of 16th century studies of perspective as well as the art and craft of that time.

Nesting Regular Polygons

The simplest example of of geometric nesting is that obtained by drawing circles around and inside simple planar shapes. In particular, every regular polygon has both an incircle (an internal circle tangent to its sides) and a circumcircle (an external circle passing through all its vertices). Here they are illustrated for the equilateral triangle:

In[]:=

With{triangle=RegularPolygon[3]},Graphics

styling

,triangle,Circumsphere[triangle],Insphere[triangle],

labels

,

opts



Out[]=

By suitably choosing the circumcircle of one shape to correspond to the incircle of the next, it is possible to nest regular polygons centered at the origin (corresponding to the position of the Sun in a heliocentric model). This process is easily illustrated as follows, where the Wolfram Function Repository resource function nests a sequence of four random n-gons:

In[]:=

sun=

style

,FaceForm

,Disk[{0,0},.02];

In[]:=

SeedRandom[21];Show[{Graphics[sun],ResourceFunction["NestedIncirclePolygons"][RandomInteger[{3,8},4]]}]

Out[]=

Kepler attempted to apply exactly this process to geometrically explain the distances between planetary orbits:

Out[]=

Kepler's approach

nested shapes

solar system?

Unfortunately, despite having infinitely many regular polygons, even though only six planets were known at the time:

In[]:=

EntityList

planets known before Herschel's discovery of Uranus

PLANETS



Out[]=



Mercury

Venus

Earth

Mars

Jupiter

Saturn



… and despite the fact that different nestings of polygons can give many different combinations of orbit sizes in this model:

In[]:=

SeedRandom[7];Table[Show[{Graphics[sun],ResourceFunction["NestedIncirclePolygons"][RandomInteger[{3,8},4]]}],{4}]

Out[]=





… Kepler found no combination possible that matched their orbits, plotted here as approximated by circles of radius equal to their mean orbital distances:

In[]:=

Graphicssun,Function[{r,glyph},Tooltip[Circle[{0,0},QuantityMagnitude[r]],glyph]]@@@EntityValue

planets known before Herschel's discovery of Uranus

PLANETS

,{"AverageOrbitDistance","Glyph"}

Out[]=

This is actually not surprising since for a triangle, the circumcircle is much bigger than the incircle, while for a polygon with a large enough number of sides, these two circles are not too different in size:

GraphicsRowTableGraphics

style

,Through[{Identity,Circumsphere,Insphere}[RegularPolygon[n]]],{n,{3,7}}

Out[]=

In particular, the leap from Jupiter's orbit to that of Mars cannot be achieved by regular polygons since there is no regular n-gon with vertices lying on Jupiter's (assumed circular) orbit, which has Mars's (again assumed circular) orbit as its incircle:

In[]:=

Module{rj,rm},{rj,rm}=QuantityMagnitudeEntityValue

Jupiter

PLANET

Mars

PLANET

,

average orbit distance

;GraphicsCircle[{0,0},#]&/@{rj,rm},

style

,Table[RegularPolygon[rj,p],{p,3,7}]

Out[]=

Nesting Regular Solids

Undeterred, Kepler decided to try nesting solids in three dimensions. In 2D, shapes are built out of 1D lines. Increasing the dimension to 3D, shapes are built out of 2D faces. So then a regular polyhedron needs to have all faces the same shape, all edges the same length and all angles where faces meet be the same. This means that the faces also must be regular polygons.

As in 2D, there is an easy procedure to generate regular polyhedra. Start with the smallest regular polygon (the equilateral triangle), adjoin additional copies as depicted below and fold those. There are only three folding angles β leading to regular polyhedra. These are the tetrahedron, the octahedron and the icosahedron. Now do the same for the square. There is only one folding angle that works,

β90°

, generating the cube. The next regular polygon is a pentagon with only a unique angle β generating the dodecahedron. Notice now that for the regular hexagon and beyond, extra copies leave no room for folding them without making undesired overlaps. Therefore, this procedure does not generate any additional polyhedra:

As shown by the procedure of folding regular polygons (see Espigulé Pons 2013), there is not an infinite number of regular polytopes in 3D as in 2D. Rather, there are exactly five: the tetrahedron, hexahedron (cube), octahedron, dodecahedron and icosahedron. See for example the beautiful illustrations of the five Platonic solids as drawn by Leonardo da Vinci for Pacioli's work De divina proportione:

To Plato and his contemporaries these objects were the ultimate embodiment of mathematical beauty and perfect symmetry. They believed that each one represented an element of nature, therefore playing an important role in the structure of the universe.

Now, think about the 3D equivalents of the incircle and circumcircle—the insphere and circumsphere. The insphere is the biggest sphere contained inside the 3D shape, and it just touches the center of each face:

In[]:=

platonics={Tetrahedron,Octahedron,Icosahedron,Cube,Dodecahedron};

In[]:=

GraphicsRowTableGraphics3DOpacity[0.5],

,solid[],

,Insphere[solid[]],

opts

,{solid,platonics}

Out[]=

The circumsphere is the smallest sphere that surrounds the whole shape and touches each of the vertices:

In[]:=

GraphicsRowTableGraphics3DOpacity[0.5],

,solid[],

,Circumsphere[solid[]],

opts

,{solid,platonics}

Out[]=

Just as in 2D, these 3D shapes can be nested inside each other so that the circumsphere of one shape lines up with the insphere of the next. Each Platonic solid also has a unique ratio of the sizes of these two spheres. Bear in mind that while there are an infinite number of these ratios available for building a solar system in 2D, there are only five in 3D, thus giving a finite number of distinct ways in which those solids can be nested.

Johannes Kepler therefore suggested the following arrangement with two of these solids nested inside the sphere corresponding to Earth's orbit and the other three circumscribed outside it:

Out[]=

The following sections show how this procedure is accomplished.

Earth

Step 1: "The Earth's sphere is the measure of all other orbits."

The astronomical unit is a natural scale for expressing sizes in the solar system, as 1 au corresponds roughly to the average orbital distance of the Earth:

In[]:=

Earth

PLANET



average orbit distance



Out[]=

1.00013973

Therefore, for the purposes of this model, consider the radius of the Earth's orbit to be 1:

In[]:=

rearth=1;

To aid in constructing visualizations, define some plotting functions:

In[]:=

OrbitPlot[r_,col_,shape_]:={col,Tube[Table[r{Cos[a],Sin[a],0},{a,2Pi/3,7Pi/3,.01}]],shape}

In[]:=

OpenSphere[r_,f_]:=SphericalPlot3Dr,{θ,(1-f)Pi,Pi},{ϕ,2Pi/3,7Pi/3},

opts

[[1]]

In[]:=

Radius[Sphere[_,r_]]:=rCircumradius[poly_]:=Radius[Circumsphere[poly]]

In[]:=

Tubify[poly_,r_:.03]:=MeshPrimitives[CanonicalizePolyhedron[poly],1]/.Line[x_]Tube[x,rCircumradius[poly]]

In[]:=

$PlotOptions=

opts

;

Now plot a sphere with radius equal to that of the Earth's orbit centered on the Sun:

In[]:=

sun=

,Sphere[{0,0,0},.05];earth=OrbitPlotrearth,

,Sphere

dims

;

In[]:=

Graphics3D[{sun,earth,OpenSphere[rearth,1]},$PlotOptions]//Rasterize

Out[]=

The Outer Planets

Step 2: "Circumscribe a dodecahedron around it. The sphere surrounding it will be that of Mars."

In order to outwardly nest, first find the edge length of the solid to nest. For example, a dodecahedron circumscribed around the sphere representing the Earth would have side length:

In[]:=

Radius[Sphere[_,r_]]:=rCircumradius[poly_]:=Radius[Circumsphere[poly]]Inradius[poly_]:=Radius[Insphere[poly]]

In[]:=

lmars=rearth/Inradius[Dodecahedron[]]//FunctionExpand//FullSimplify

Out[]=

50-22

The corresponding planet radius corresponding to a sphere circumscribed around the dodecahedron would then have radius:

In[]:=

rmars=lmarsCircumradius[Dodecahedron[]]//FunctionExpand//FullSimplify

Out[]=

15-6

In[]:=

dodeca=

,Tubify@Dodecahedron

dims

;mars=OrbitPlotrmars,

,Dodecahedron

dims

;

In[]:=

Graphics3D[{sun,earth,mars,dodeca,OpenSphere@@@{{rearth,1},{rmars,1/2}}},$PlotOptions]//Rasterize

Out[]=

Step 3: "Circumscribe a tetrahedron around Mars. The sphere surrounding it will be that of Jupiter."

In[]:=

ljupiter=rmars/Inradius[Tetrahedron[]]//FunctionExpand//FullSimplify

Out[]=

10-4

In[]:=

rjupiter=ljupiterCircumradius[Tetrahedron[]]//FunctionExpand//FullSimplify

Out[]=

15-6

In[]:=

tetra=

,Tubify@Tetrahedron

dims

;jupiter=OrbitPlotrjupiter,

,Tetrahedron

dims

;

In[]:=

Graphics3D[{sun,earth,mars,tetra,jupiter,OpenSphere@@@{{rearth,1/2},{rmars,1},{rjupiter,1/2}}},$PlotOptions]//Rasterize

Out[]=

Step 4: "Circumscribe a cube around Jupiter. The surrounding sphere will be that of Saturn."

In[]:=

lsaturn=rjupiter/Inradius[Cube[]]//FunctionExpand//FullSimplify

Out[]=

15-6

In[]:=

rsaturn=lsaturnCircumradius[Cube[]]//FunctionExpand//FullSimplify

Out[]=

5-2

In[]:=

cube=

,Tubify@Cube

dims

;saturn=OrbitPlotrsaturn,

,Cube

dims

;

In[]:=

Graphics3D[{sun,earth,mars,jupiter,cube,saturn,OpenSphere@@@{{rearth,1/2},{rmars,1/2},{rjupiter,1},{rsaturn,1/2}}},$PlotOptions]//Rasterize

Out[]=

The Inner Planets

Step 5: "Now, inscribe an icosahedron inside the orbit of the Earth. The sphere inscribed in it will be that of Venus."

In[]:=

lvenus=rearth/Circumradius[Icosahedron[]]//Simplify

Out[]=

In[]:=

rvenus=lvenusInradius[Icosahedron[]]//FullSimplify

Out[]=

(5+2

)

In[]:=

ico=

,Tubify@Icosahedron

dims

;venus=OrbitPlotrvenus,

,Icosahedron

dims

;

In[]:=

Graphics3D[{sun,earth,ico,venus,OpenSphere@@@{{rearth,1/2},{rvenus,1}}},$PlotOptions]//Rasterize

Out[]=

Step 6: "Inscribe an octahedron inside Venus. The sphere inscribed in it will be that of Mercury."

In[]:=

lmercury=rvenus/Circumradius[Octahedron[]]

Out[]=

(5+2

)

In[]:=

rmercury=lmercuryInradius[Octahedron[]]//Simplify

Out[]=

In[]:=

octa=

,Tubify@Octahedron

dims

;mercury=OrbitPlotrmercury,

,Octahedron

dims

;

In[]:=

Graphics3D[{sun,earth,venus,octa,mercury,OpenSphere@@@{{rearth,1/2},{rvenus,1/2},{rmercury,1}}},$PlotOptions]//Rasterize

Out[]=

Inner and Outer Combined

Including both inner and outer nestings gives beautiful illustrations of Kepler's nestings:

Out[]=

Kepler's Diagram

After these investigations, it is now possible to reproduce Kepler's famous diagram with the aid of a few visualization functions:

In[]:=

HalfSphericalShell[r_,t_]:=Module{range=Sort[N@{r,r+t}]},HatchShading[.4],ParametricPlot3D#{Cos[q],Sin[q],0}&/@range,{q,0,2π},

opts

[[1]],

style

,DiscretizeRegionSphericalShell[range],Max[range]{{-1,1},{-1,1},{-1,0}},

opts



In[]:=

$PlotOptions={BoxedFalse,Lighting"Neutral",Method{"ShrinkWrap"True}};

Here is a visualization of the nesting of inner planets:

In[]:=

(inner=Graphics3D[{HalfSphericalShell[#,-.1]&/@{rearth,rvenus,rmercury},ResourceFunction["RibbonPolyhedron"][#,.05][[1]]&/@{Octahedron[lmercury],Icosahedron[lvenus]}},$PlotOptions])//Rasterize

Out[]=

Construct the dashed lines corresponding to face diagonals of the cube in Kepler's drawing:

In[]:=

CubeFaceDiagonals=Thin,AbsoluteDashing[3],LineSelectSubsetsMeshPrimitivesCanonicalizePolyhedronCube

5π

,0,lsaturn,0[[All,1]],{2},EuclideanDistance@@#

lsaturn&;

In[]:=

Graphics3DCube

5π

,0,lsaturn,CubeFaceDiagonals,BoxedFalse,ImageSizeSmall

Out[]=

… and combine with polyhedra and half-shells to depict the nesting of outer planets:

In[]:=

outer=Graphics3DHalfSphericalShell@@@{{rmars,.3},{rjupiter,.3},{rsaturn,.9}},ResourceFunction["RibbonPolyhedron"]@@@{Dodecahedron[{.2,0},lmars],.1},{Tetrahedron[{-.7,0},ljupiter],.25},Cube

dims

,.35[[All,1]],CubeFaceDiagonals,$PlotOptions//Rasterize

Out[]=

Combining both diagrams gives a modern version of Kepler's famous figure:

In[]:=

(KeplersModel=Show[{inner,outer}])//Rasterize

Out[]=

For a more direct comparison, take Kepler's image:

In[]:=

img=

;

… create a mask for the background and use it to inpaint the foreground:

In[]:=

mask=ColorNegate@Erosion[Binarize[img],2];

In[]:=

Show[background=Inpaint[img,mask],ImageSizeSmall]

Out[]=

… do a little image processing to recolor the rasterized image and get the transparent regions of the model:

In[]:=

r=Rasterize[KeplersModel,RasterSizeImageDimensions[img]];a=AlphaChannel@Rasterize[KeplersModel,RasterSizeImageDimensions[img],BackgroundNone];

… and finally compose the transparent recolored image with the generated background and display side by side with Kepler's original:

In[]:=

GraphicsRowShow#,

size

&/@{ImageCompose[background,SetAlphaChannel[HistogramTransform[r,img],a]],img}

Out[]=

The agreement is remarkable.

Kepler's Planetary Radii

To summarize Kepler's construction for the inner planets, inscribe an icosahedron and octahedron, then the circumradii of the resulting spheres to give the orbital radii of Venus and Mercury, respectively. This can be computed by considering unit edge-length solids and then accumulating the insphere-to-circumsphere ratios by multiplication:

Radius[Sphere[_,r_]]:=rCircumradius[poly_]:=Radius[Circumsphere[poly]]Inradius[poly_]:=Radius[Insphere[poly]]

In[]:=

InnerPlanetRatios=FoldList[Times,Table[Divide@@Through[{Inradius,Circumradius}[solid[]]],{solid,{Icosahedron,Octahedron}}]]//FullSimplify

Out[]=



(5+2

)



Similarly, for the outer planets, circumscribe a dodecahedron, tetrahedron and cube; the inradii of the resulting spheres give the orbital radii of Mars, Jupiter and Saturn, respectively. Computing as before but this time accumulating circumsphere-to-insphere ratios by multiplication:

In[]:=

OuterPlanetRatios=FoldList[Times,Table[Divide@@Through[{Circumradius,Inradius}[solid[]]],{solid,{Dodecahedron,Tetrahedron,Cube}}]]//FunctionExpand//FullSimplify

Out[]=



15-6

5-2



Combining the inner and outer ratios with the assumed unit radius of the Earth's orbit gives the following symbolic ratios for Kepler's construction:

In[]:=

rplatonic=Join[Reverse[InnerPlanetRatios],{1},OuterPlanetRatios]

Out[]=



(5+2

)

,1,

15-6

5-2



Numericizing:

In[]:=

N[rplatonic]

Out[]=

{0.458794,0.794654,1.,1.25841,3.77523,6.53888}

If these values agree with the actual planetary radii, Kepler's labors have been rewarded:

In[]:=

rplanets=QuantityMagnitude

planets known before Herschel's discovery of Uranus

PLANETS

["AverageOrbitDistance"];

A quick comparison shows that while they are not too far off, they are also not all that close. For closer inspection, compare in several different forms—as a table:

In[]:=

TableFormTranspose[{rplatonic,N[rplatonic],rplanets}],

opts



Out[]//TableForm=

	exact Platonic radius	approximate	actual mean distance form sun
Mercury	1 9 + 2 9 5	0.458794	0.39528297
Venus	1 15 (5+2 5 )	0.794654	0.72334858
Earth	1	1.	1.00013973
Mars	15-6 5	1.25841	1.53030994
Jupiter	3 15-6 5	3.77523	5.20945576
Saturn	9 5-2 5	6.53888	9.5510530

… on a semi-log plot:

In[]:=

ListLogPlot{rplatonic,rplanets},

opts



Out[]=

	Kepler's Platonic estimate
	actual distance from Sun (AU)

… and as circular orbital paths:

In[]:=

LabeledGraphicsThick,

circle segment

/@rplatonic,

circle segment

/@rplanets,LineLegend

,{"Kepler's estimate","actual mean distance"},Bottom

Out[]=

	Kepler's estimate
	actual mean distance

While the alignment is far from perfect, it is nonetheless surprising that the sizes of planetary orbits are even close to such an abstract geometrical theory. The fact that the agreement is as close as it is led Kepler to believe he had revealed God's plan for the universe through perfect geometry.

Metaphysical Ordering

Kepler's ordering included a number of metaphysical constraints. In particular, Kepler believed the Earth should separate the solids that can "float" (i.e. the octahedron and icosahedron) from those that "stand upright" (i.e. the cube, tetrahedron and dodecahedron). Furthermore, since the cube is characterized by a single angle (the right angle), Kepler believed this property symbolized the solitude associated with Saturn. While there are a total of 120 (5! = five factorial) ways to nest the five Platonic solids:

In[]:=

platonics={Tetrahedron,Octahedron,Icosahedron,Cube,Dodecahedron};

… a quick computation shows that these constraints reduce the number of possible orderings from 120 total to precisely these four:

In[]:=

metaphysicalpermutations=With[{floating=Octahedron|Icosahedron,standing=Tetrahedron|Dodecahedron|Cube},Select[Permutations[platonics],MatchQ[{floating,floating,standing,standing,Cube}]]]

Out[]=

{{Octahedron,Icosahedron,Tetrahedron,Dodecahedron,Cube},{Octahedron,Icosahedron,Dodecahedron,Tetrahedron,Cube},{Icosahedron,Octahedron,Tetrahedron,Dodecahedron,Cube},{Icosahedron,Octahedron,Dodecahedron,Tetrahedron,Cube}}

To investigate how well these orderings approximate planetary orbital radii, compose a few lines of Wolfram Language code:

In[]:=

OrbitDistance[solid_]:=Divide@@Through[{Circumradius,Inradius}[solid[]]]OrbitDistances[solids_]:=Table[OrbitDistance[solid],{solid,solids}]

In[]:=

PlatonicNesting[solids_]:=Module[{inner=FoldList[Times,1/OrbitDistances[Reverse@Take[solids,2]]],outer=FoldList[Times,OrbitDistances[Drop[solids,2]]]},Join[Reverse[inner],{1},outer]//FunctionExpand//FullSimplify]

Applying this function to Kepler's ordering:

In[]:=

KeplerOrdering={Octahedron,Icosahedron,Dodecahedron,Tetrahedron,Cube};

… gives the following sequence of planetary orbital radii:

In[]:=

PlatonicNesting[KeplerOrdering]//FunctionExpand//FullSimplify

Out[]=



(5+2

)

,1,

15-6

5-2



Numericizing:

In[]:=

PlatonicNesting[KeplerOrdering]//N

Out[]=

{0.458794,0.794654,1.,1.25841,3.77523,6.53888}

Let us now apply this function to the four nestings permitted by Kepler's cosmology and compute their deviations from actual planet orbit distances:

In[]:=

rankedmetaphysical=SortBy[{#,radii=PlatonicNesting[#],EuclideanDistance[radii,rplanets]}&/@metaphysicalpermutations,Last];

As it turns out, the nestings give fits of comparable quality, with Kepler's ordering being the best of the four:

In[]:=

Position[rankedmetaphysical,KeplerOrdering][[1,1]]

Out[]=

These results are summarized in the following table in which Kepler's model is highlighted. Here, the first column is the ordered list of solids, the second is the exact orbital distances and the third column is standard deviation of the model from actual planetary radii:

In[]:=

PlatonicIcons[solids_List]:=RasterizeGraphicsRowTableGraphics3Dsolid[],

opts

,{solid,solids},

opts



In[]:=

TextGrid{PlatonicIcons[#],#2,#3}&@@@rankedmetaphysical,

opts



Out[]=

	 1 9 + 2 9 5 , 1 15 (5+2 5 ) ,1, 15-6 5 ,3 15-6 5 ,9 5-2 5 	3.3486
	 1 9 + 2 9 5 , 1 3 ,1, 15-6 5 ,3 15-6 5 ,9 5-2 5 	3.3510
	 1 9 + 2 9 5 , 1 15 (5+2 5 ) ,1,3,3 15-6 5 ,9 5-2 5 	3.6468
	 1 9 + 2 9 5 , 1 3 ,1,3,3 15-6 5 ,9 5-2 5 	3.6490

Other Platonic Solid Orderings

Since Kepler's associations between the Platonic solids and the planets were made not only on the basis of their geometrical properties, but also taking into account their astrological and metaphysical attributes, a natural question is how good that ordering is in reproducing planetary orbital radii compared to all possible 5! (5 factorial)  120 permutations of Platonic solid orderings. To answer this question, reproduce the nestings of solids as previously shown, but this time allow for arbitrary orderings.

To do this, exhaustively enumerate the set of radii for all possible orderings using the PlatonicNesting function defined previously:

In[]:=

nestings={#,radii=PlatonicNesting[#],EuclideanDistance[radii,rplanets]}&/@Permutations[platonics];

Here are the results for the first 10 permutations:

In[]:=

TextGrid[{PlatonicIcons[#],#2,#3}&@@@Take[nestings,10],DividersAll]

Out[]=

	 1 3 3 , 1 3 ,1, 15-6 5 ,3 5-2 5 ,3 15 (-2+ 5 )	7.4611
	 1 3 3 , 1 3 ,1, 15-6 5 ,15-6 5 ,3 15 (-2+ 5 )	7.7224
	 1 3 3 , 1 3 ,1, 3 ,3 5-2 5 ,3 15 (-2+ 5 )	7.4589
	 1 3 3 , 1 3 ,1, 3 ,3 5-2 5 ,3 15 (-2+ 5 )	7.4589
	 1 3 3 , 1 3 ,1, 15-6 5 ,15-6 5 ,3 15 (-2+ 5 )	7.7224
	 1 3 3 , 1 3 ,1, 15-6 5 ,3 5-2 5 ,3 15 (-2+ 5 )	7.4611
	 1 27 + 2 27 5 , 1 15 (5+2 5 ) ,1, 3 ,3,3 15-6 5 	6.1891
	 1 27 + 2 27 5 , 1 15 (5+2 5 ) ,1, 3 ,3 5-2 5 ,3 15-6 5 	6.5271
	 1 27 + 2 27 5 , 1 15 (5+2 5 ) ,1, 3 ,3,3 15-6 5 	6.1891
	 1 27 + 2 27 5 , 1 15 (5+2 5 ) ,1, 3 ,3 5-2 5 ,3 15-6 5 	6.5271

From the first few cases, several different orderings appear to give the same spacings. Closer inspection reveals that in fact, there are precisely four orderings corresponding to each possible set of distances. This follows from duality of the cube/octahedron and dodecahedron/icosahedron, which makes interchanging them equivalent in the construction process. Technically, for a Platonic solid with circumradius R, inradius r and midradius ρ and using a subscript d to denote the dual, the following identity is known to hold:

r



Therefore, the ratio of circumradius to inradius:



… (which is the only parameter on which the construction depends) is the same for dual pairs of solids:

In[]:=

With{props={"Entity","Dual","Circumradius","Inradius"}},TextGridJoin

labels

,Append[#,FullSimplify[Divide@@Take[#,-2]]]&/@EntityValue

Platonic solids

POLYHEDRA

,props,

opts



Out[]=

solid	dual	R	r	R r
regular tetrahedron	tetrahedron	3 2 2	1 2 6	3
cube	regular octahedron	3 2	1 2	3
regular octahedron	cube	1 2	1 6	3
regular dodecahedron	regular icosahedron	1 4  3 + 15 	1 20 250+110 5	15-6 5
regular icosahedron	regular dodecahedron	1 4 10+2 5	1 12 3 3 + 15 	15-6 5

Therefore, using the construction process using the five Platonic solids, only 30 (120 permutations of five objects divided by four equivalent nestings corresponding to Platonic duality of two pairs of them) distinct distance sets can be obtained.

To look more closely, sort and group the computed values by the deviation of the models from the actual planet orbit distances:

In[]:=

ranked={#[[All,1]],#[[1,2]],#[[1,3]]}&/@SplitBy[SortBy[nestings,Last],Last];

If Kepler's ordering is optimal, it will appear first in this ranks list. Checking:

In[]:=

Position[ranked,KeplerOrdering][[1,1]]

Out[]=

… reveals that Kepler's (highlighted in the following table) is the sixth best of all possible Platonic nestings:

In[]:=

TextGrid{PlatonicIcons[Last[#1]],#2,#3}&@@@Take[ranked,8],

opts



Out[]=

	 1 15 (5+2 5 ), 1 15 (5+2 5 ) ,1, 3 ,3 3 ,9	0.63672
	 1 15 (5+2 5 ), 1 15 (5+2 5 ) ,1,3,3 3 ,9	1.5889
	 1 15 (5+2 5 ), 1 15 (5+2 5 ) ,1, 3 ,3,9	2.2993
	 1 9 + 2 9 5 , 1 15 (5+2 5 ) ,1, 3 ,3 3 ,9 5-2 5 	3.0205
	 1 9 + 2 9 5 , 1 3 ,1, 3 ,3 3 ,9 5-2 5 	3.0231
	 1 9 + 2 9 5 , 1 15 (5+2 5 ) ,1, 15-6 5 ,3 15-6 5 ,9 5-2 5 	3.3486
	 1 9 + 2 9 5 , 1 3 ,1, 15-6 5 ,3 15-6 5 ,9 5-2 5 	3.3510
	 1 9 + 2 9 5 , 1 15 (5+2 5 ) ,1,3,3 3 ,9 5-2 5 	3.3530

Furthermore, the best ordering (consisting of dodecahedron/icosahedron, icosahedron/dodecahedron, cube/octahedron, tetrahedron, octahedron/cube) is much better than Kepler's. Comparing the top 8 orderings (where Kepler's is number 6) is illustrative:

In[]:=

OrbitalComparison[rplatonic_,opts___]:=GraphicsThick,

circle segment

/@rplatonic,

circle segment

/@rplanets,opts

In[]:=

LabeledOrbitalComparison[solids_,radii_]:=OrbitalComparison[radii,PlotLabelPlatonicIcons[solids]]

In[]:=

GridPartition[LabeledOrbitalComparison[First[#1],#2]&@@@Take[ranked,8],UpTo[4]],

spacing

//Rasterize

Out[]=

Other Resources

History of Mathematics
Da Vinci's Polyhedra

Wolfram Demonstration
Kepler's Harmonices Mundi

Wolfram Demonstration
Kepler's Mysterium Cosmographicum

Additional Reading

Brecher, K. "Kepler’s Mysterium Cosmographicum: A Bridge Between Art and Astronomy?" In Proceedings of Bridges 2011: Mathematics, Music, Art, Architecture, Culture. Tessellations Publishing, pp. 379–386, 2011.
Caspar, M. Kepler. New York: Dover, 1993.
Espigulé Pons, B. "Unfolding Symmetric Fractal Trees." Proceedings of Bridges 2013: Mathematics, Music, Art, Architecture, Culture, pp. 295–302, 2013.
Field, J. V. Kepler's Geometrical Cosmology. Chicago: University of Chicago Press, 1988.
Kepler, J. Mysterium Cosmographicum. Tübingen, Germany: Georgius Gruppenbachius, 1596.
Livio, M. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. New York: Broadway Books, pp. 142–158, 2002.
Pappas, T. The Joy of Mathematics: Discovering Mathematics All Around You. San Carlos, CA: Wide World Publishing/Tetra, pp. 110 and 180, 1989.