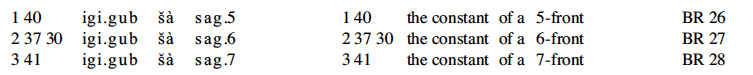around 1900–1600 BCE
Susa Mathematical Tablets
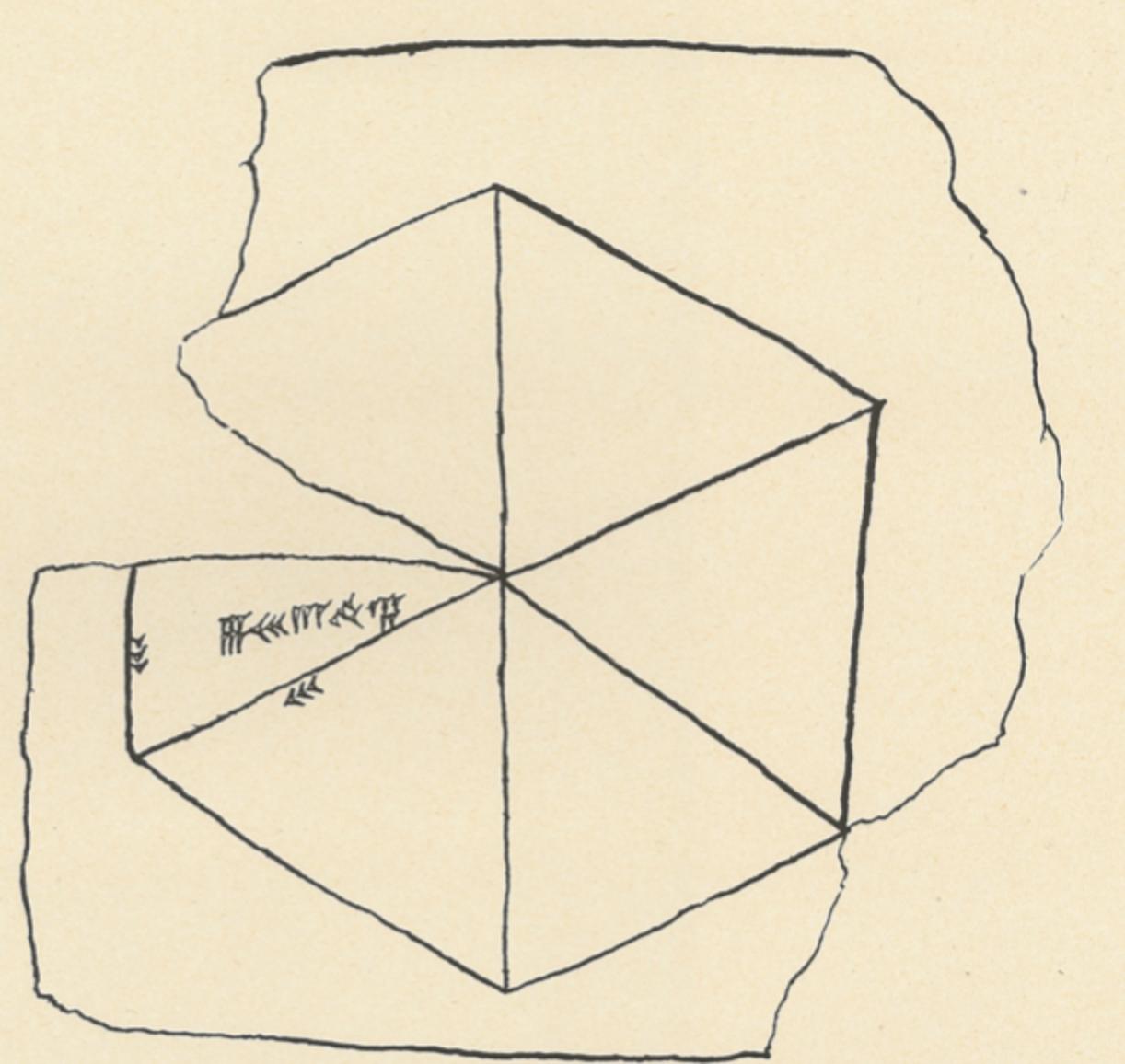
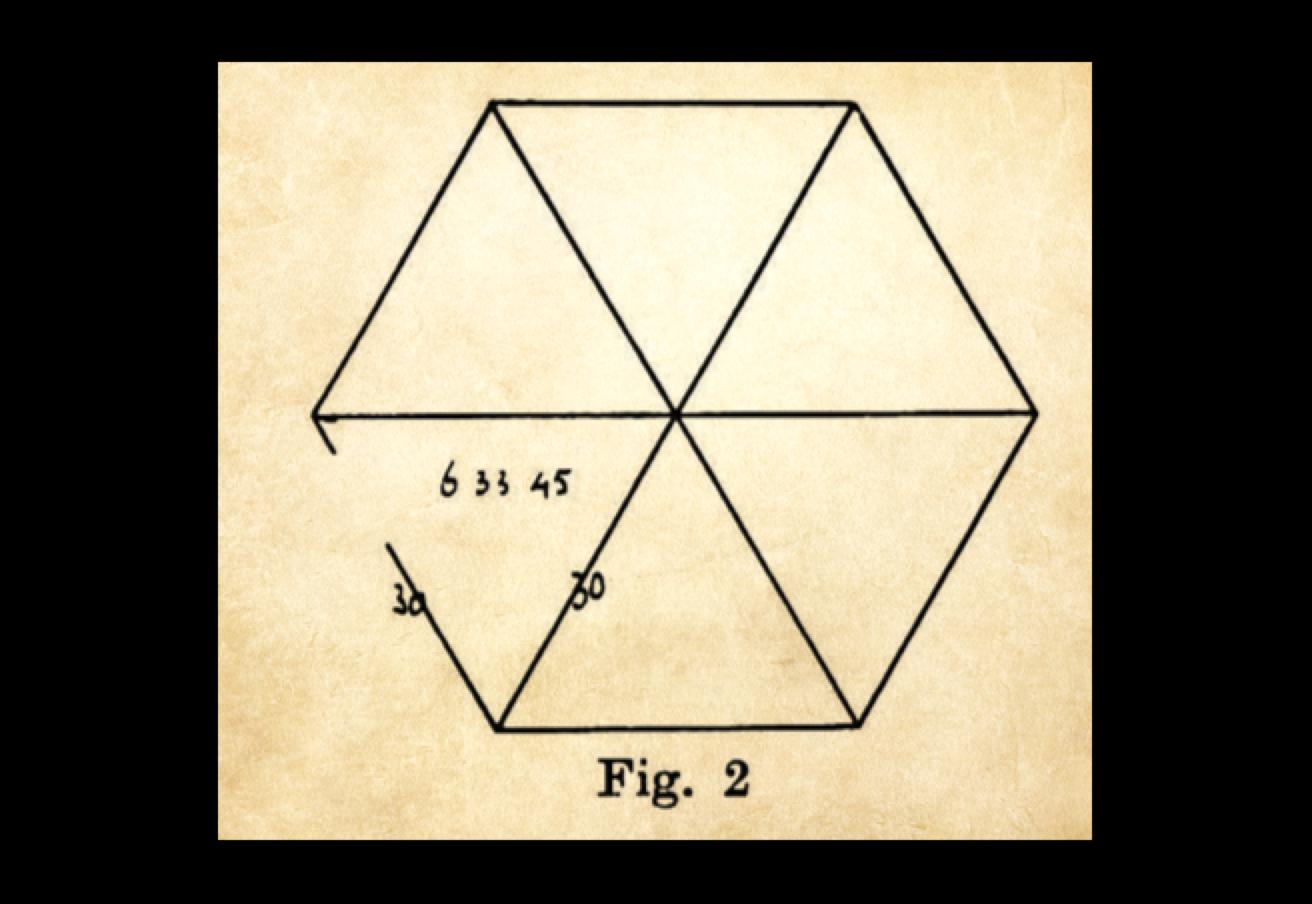
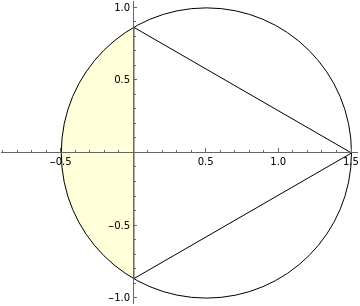
Babylonian approximation to π based on a regular hexagon
In 1933, a total of 26 mathematical tablets were excavated some two hundred miles from Babylon in the ancient Elamite city of Susa. The tablets are believed to date from between 1900 and 1600 BCE and contain a number of interesting geometric figures and mathematical constants arising from geometric computations. Partial translations of the tablets were published in 1950, but the first detailed analysis of three particularly interesting tablets did not appear until 1961.

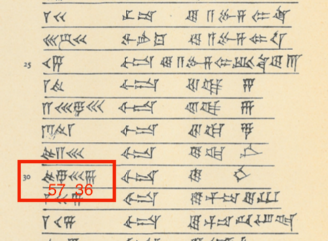
The tablets referred to as TMS 2 and TMS 3 are of particular interest. TMS 2 is relatively straightforward, containing a diagram of a regular hexagon and markings that give an approximation to the area of an equilateral triangle. TMS 3, on the other hand, contains a tabular list of geometric constants corresponding to many shapes, including polygons but also featuring many more complicated geometric shapes, including the semicircle (termed a crescent) and lens-shaped figures known to the Babylonians as the ox-eye and grain figure (or grain-field, or barleycorn). The tabulation includes 68 constants spread over the 71 lines. On line 30, the perimeter-to-circumcircle circumference ratio for a regular hexagon is given as 24/25, which implies perhaps the world's oldest recorded approximation to π with value 3 + 1/8 = 3.125.